Hahn embedding theorem

In mathematics, especially in the area of abstract algebra dealing with ordered structures on abelian groups, the Hahn embedding theorem gives a simple description of all linearly ordered abelian groups.

The theorem states: Any linearly ordered abelian group G can be embedded as an ordered subgroup of the additive group ℝΩ endowed with a lexicographical order, where ℝ is the additive group of real numbers (with its standard order), and Ω is the set of Archimedean equivalence classes of G.

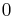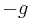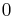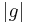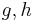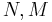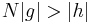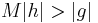Let 0 denote the identity element of G. For any nonzero g∈G, exactly one of the elements g or -g is greater than 0; denote this element by |g|. Two nonzero elements g,h∈G are Archimedean equivalent if there exist natural numbers N,M∈ℕ such that N |g| > |h| and M |h| > |g|. (Heuristically: neither g nor h is "infinitesimal" with respect to the other). The group G is Archimedean if all nonzero elements are Archimedean-equivalent. In this case, Ω is a singleton, so ℝΩ is just the group of real numbers. Then Hahn's Embedding Theorem reduces to Hölder's theorem (which states that a linearly ordered abelian group is Archimedean if and only if it is a subgroup of the ordered additive group of the real numbers).

(Gravett 1956) gives a clear statement and proof of the theorem. The papers of (Clifford 1954) and (Hausner & Wendel 1952) together provide another proof. See also (Fuchs & Salce 2001, p. 62).

References